EM2 NA Overview Brochure 2025

Exponentially Greater Aha Moments

PreK–Algebra I Program Overview

Exponentially Greater Aha Moments

All students deserve access to engaging, knowledgebuilding instruction—and all teachers deserve the tools and support to deliver it.

Educators are called to provide a more equitable, rigorous, and relevant learning environment for their students so every student can experience aha learning moments that lead to conceptual understanding of math.

Eureka Math2® empowers educators with lessons and tools that simplify implementation with a coherent design while ensuring students become confident doers of math.

Research Proven Results

Eureka Math2 takes the very best from years of user research, efficacy data, and in-the-classroom teacher testing to create a new program built for students and teachers.

KEY FINDING 1

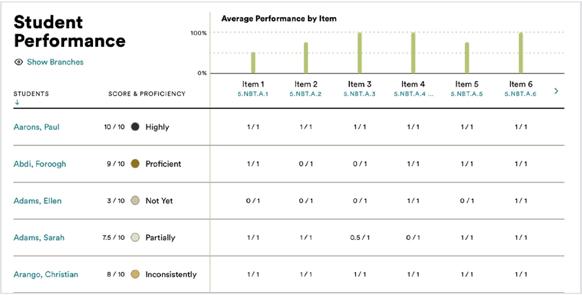
Math proficiency increased dramatically.

Scoring as Proficient or Advanced on

KEY FINDING 2

The percentage of students exceeding typical growth increased year-over-year, indicating that the impact of Eureka Math2 increases over time.

KEY FINDING 3

The students who were the least proficient saw the greatest gains with Eureka Math2. This effect appears to increase over time.

Students Exceeding Typical Growth on MAP Math Assessment

Coherent Design

We believe in empowering teachers to ensure rich student engagement and discourse. To facilitate that, the Eureka Math2 program design integrates a strategic blend of instructional approaches.

A STRATEGIC BLEND OF INTENTIONAL APPROACHES

COGNITIVELY GUIDED

Students draw on existing knowledge to grow their conceptual understanding through discovery opportunities, videos, instructional routines, rigorous open-middle and open-ended tasks, and more.

STUDENT CENTERED

Students actively communicate their thinking and reasoning as they gain the confidence to think like mathematicians and see themselves as fully capable learners.

EXPLICIT & SYSTEMATIC

Concepts are sequenced in a coherent way so students consistently build knowledge and skills while engaging in guided experiences, instructional routines, and distributed and interleaved practice.

and counted. friend count? what they already counted. one (cube) only once. they lined them up.

Compare

path, Unifix Cubes; S: Large number path to organize, count, and compare. numbered side up, to each student.

MATHEMATICAL PRACTICE

The Eureka Math2 teacher-writers know that teachers need a coherent program that can support all their learners and help them build habits of mind to think mathematically.

Differentiation: Support

Consider making brief mention of incorrect counting behaviors, such as

That’s why the mathematical practices are embedded in every Eureka Math2 lesson—ensuring students develop a deep, flexible, and enduring understanding of mathematics.

number path. Have students follow along on their own on each number, and count out loud. When the class clear their number paths and repeat the process to organize

EFFECTIVE TEACHING PRACTICES

7 8 9 10 11 12 13 14 15 16 17 18 19 20

The Standards of Mathematical Practice describe the actions that student should develop to become effective mathematical thinkers. By engaging in

finish, guide a class discussion. your last cube. That number is the total. Tell a partner

help you organize your cubes?

path make it easier to find the total? cube shows the total, so I don’t have to count. aside and turn their attention to the class number path. Place cubes of another color along the bottom.

• placing more than 1 cube in a space,

• skipping numbers on the number path as you place cubes, or

• starting at a number other than 1 when placing cubes.

Promoting the Standards for Mathematical Practice

When students use the number path and are careful to start at 1, not skip any spaces, and only put 1 item in each space, they attend to precision (MP6)

Ask the following questions to promote MP6:

• When using the number path, what do you need to be extra careful with?

• What mistakes are easy to make when using the number path?

DESIGNED TO SIMPLIFY IMPLEMENTATION

Eureka Math2 is designed by teachers and for teachers, offering smooth implementation and maximized student support.

Every lesson opens with the Lesson at a Glance, which includes key questions and achievement descriptors. This structure helps teachers anchor their instruction to the intended outcomes and gives students clear learning expectations.

In addition, every lesson simplifies implementation with a clear plan that shows teachers an agenda for the learning and a description for any required preparation. A list of materials is also included. The Teach book gives teachers an easy-tofollow guide so their focus can remain on their students.

Eureka Math2 lessons follow a research-backed structure to help students manage their cognitive load and engage in richer learning so they build enduring knowledge.

LESSON FLOW

Each lesson begins with daily practice that builds procedural fluency and anticipates the conceptual learning of the lesson. FLUENCY

LAUNCH

This section sets a goal for the day’s learning and readies students for rigorous thinking often using an instructional routine.

LEARN

This section develops conceptual understanding of new content and includes application of learning in the Problem Set.

LAND

Students articulate their understanding of the day’s content by answering key questions and completing an Exit Ticket.

A smooth implementation requires student materials to be clear and easy for students to use. Sharing studentfriendly learning objectives visually and verbally helps all students grow their understanding, especially those who are not yet proficient with math concepts. Sharing and explaining learning objectives can

• help students gauge their progress,

• increase both motivation and time spent on tasks, and

• better equip students to make decisions about how to approach tasks.

DIGITAL TOOLS THAT ENHANCE AND STREAMLINE INSTRUCTION

The digital side of Eureka Math2 is there to support teachers with daily instruction, not add one more element to their classroom management load. Daily lesson slides, implementation support videos, and other teaching resources are organized to streamline teaching.

Cognitive Engagement

Through collaboration, Eureka Math2 students are cognitively engaged, and the benefits are clear.

Engagement is about much more than scoring points on a computer game or watching a simulation. Cognitive engagement occurs when students are intellectually, socially, and emotionally invested in making sense of mathematics, and it leads to an enduring and conceptual understanding of math.

BUILDS SOCIAL AND COMMUNICATION SKILLS

Collaborating with peers provides students with opportunities to develop and hone their talking and listening skills—skills that are essential beyond the classroom.

ENHANCE DEEP THINKING THROUGH PEER DISCOURSE

Talking through math strategies promotes metacognition and conceptual understanding and enables students to learn new approaches to solving problems from their peers.

SUPPORTS LANGUAGE DEVELOPMENT

All students, particularly multilingual learners, benefit from opportunities to speak and hear academic language in context.

PROMOTES SHARED KNOWLEDGE CONSTRUCTION

When students contribute their different perspectives and strategies, learning becomes less about who got it right and more about shared sense-making.

FOSTERS A POSITIVE MATH IDENTITY

With low floor/high ceiling learning opportunities, everyone has a chance to add their voice. This makes students feel valued, capable, and like they are contributing to the class’s shared understanding.

We know that connecting math to a student’s real world increases engagement, which is why we’ve created Data Talks and Data Investigations. These activities provide an opportunity for students to dive into data that’s relevant in their world and to work together to make sense of it.

In a world that is always connected, it’s becoming increasingly critical that students develop basic data science literacy skills to make informed decisions and meet the demands of a modern mathematical society. Formulate a Statistical Investigative Question

1 STATISTICAL INVESTIGATIVE PROCESS

2 Collect or Consider Data 3 Analyze

DATA TALKS

Data Talks are short activities that expose students to data. Data Talks allow students to interpret data visualizations, build the skills to make observations and ask questions, and develop the critical-thinking skills they need to interpret the data surrounding them every day.

DATA INVESTIGATIONS

Data Investigations are multi-day activities that empower students to explore the full statistical investigative process—from asking questions to collecting, interpreting, and reporting on the findings.

Confident Learning

Learner variability in classrooms is the norm. We know that equity begins with access, which is why Eureka Math2 ensures that all students are given the opportunity to confidently engage and succeed by proactively removing learning barriers through incorporation of the Universal Design for Learning (UDL) principles.

UNIVERSAL DESIGN FOR LEARNING PRINCIPLES

PROVIDE MULTIPLE MEANS OF ENGAGEMENT

Learners differ markedly in the ways in which they can be engaged or motivated to learn. Use a variety of methods to engage students. For example, provide choice, address student interest, and arrange for students to monitor their own learning, such as with goal setting, selfassessment, and reflection.

Materials—T: Large number path

Students generate data by selecting one of two choices.

Gather students and invite them to get to know one another better through a survey. As you ask questions, acknowledge their responses, but do not record their choices. Explain to students that they should raise their hands only once.

Let’s collect information about the things we like. Which do you like better: listening to stories or listening to music?

Raise your hand if you like listening to stories.

Raise your hand if you like listening to music.

I’m getting so much good information, but I need a way to organize your choices so that we can remember them and talk about what we notice.

Universal Design for Learning: Engagement

Sharing favorite activities through a class survey engages students by tapping into their interests and experiences. This also supports the development of a community of learners as students get to know their classmates and discover common interests.

Display a number path. Help students recall that they used the number path to count and compare in lesson 1.

When simplifying in this lesson, we will apply as many properties of exponents as needed so the final answer has only prime bases and only positive exponents. The bases 2, 3, and 5 are all prime and all of their exponents are positive, so we know the expression is fully simplified.

Assign problems 4 and 5. Consider working as a class to complete problem 4. Then have students complete problem 5 individually or with a partner.

Let’s count and compare your choices by using the number path. Are we able to put ourselves on the number path just as we put the Unifix Cubes on the number path? Why?

Consider adjusting the questions to match the class’s interests.

No, because we’re too big (or it’s too small).

Universal Design for Learning: Representation

How can we use the number path to show your choices?

For problems 4 and 5, simplify the expression by using the fewest number of prime bases.

We can count our hands and then put cubes on two number paths.

Transition to the next segment by framing the work.

Direct instruction on squares and cubes is in module 1 topic D. However, students have seen these numbers in grades 6 and 7. To activate prior knowledge, create and display a chart with common squares and cubes.

PROVIDE MULTIPLE MEANS OF REPRESENTATION

Today, we will use number paths to organize, show, and compare our choices.

Learners differ in the ways they perceive and comprehend information that is presented to them. Use a variety of strategies, instructional tools, and methods when presenting information and content.

eights

How could we find 4 eights if we don’t know our eights?

We can count by fours 8 times.

4 eights is the same number as 8 fours, and I know 8 fours is 32

Continue with a similar process to find 4 × 6 and 4 × 9. Support students in seeing that the rows and the columns can represent either the number of groups or the number in each group.

Invite students to turn and talk about how the commutative property can help solve unfamiliar facts.

PROVIDE MULTIPLE MEANS OF ACTION & EXPRESSION

Tape Diagrams to Represent an Array

Students draw tape diagrams to represent the rows and columns in an array. Tell students that just like the cubes and arrays, tape diagrams can also show equal groups.

Learners differ in the ways they can navigate a learning environment and express what they know. Offer students a variety of strategies and instructional tools and allow for multiple ways to demonstrate new understanding.

Let’s relate our fours array to tape diagrams. Show the 10 fours tape diagram.

Universal Design for Learning: Action & Expression

Continue to provide students with the option to use interlocking cubes as they transition to the tape diagram. While some students may prefer the use of tape diagrams immediately, others might favor the familiarity of the interlocking cubes until the factors get larger and they recognize the efficiency of tape diagrams. Providing a choice of representations allows students to express learning in flexible ways. What multiplication equation can we use to represent this tape diagram, where the first factor is the number of groups?

Eureka Math² is the only math curriculum to receive a CAST certification for accessibility and product design.

We are transforming equity in math education—ensuring every child builds lasting math knowledge.

To learn more, visit gmgre.at/em2-cast.

MULTILINGUAL LEARNERS:

In an equitable classroom, math is not just about solving problems—it’s about engaging in discussions where students reason, explain, and justify math ideas using academic language. This helps multilingual learners (MLLs) develop both math reasoning and academic English, which in turn builds students’ math confidence.

Thinking Tool

flexible grouping terminology, (problem-based different cultures,

Talking Tool

I

I

INSTRUCTIONAL ROUTINES

Instructional routines are woven throughout the curriculum and can be used flexibly whenever there are opportunities to support students with collaborative, interpretive, and productive language.

LANGUAGE SUPPORT

Language supports are embedded into the instructional design so all students can access grade-level content. These supports help teachers meet the needs of diverse learners while providing all students with access to extension opportunities and on-level learning.

LANGUAGE SCAFFOLDING

The Talking Tool supports multilingual learners in discourse and language production while the Thinking Tool supports metacognition.

ENGAGING FAMILIES AND COMMUNITIES

Family involvement plays a key role in extending learning beyond the classroom. Eureka Math2 provides families with the guidance they need to create a supportive environment where students can continue to develop their skills outside the classroom.

ASSESSMENTS: VISIBILITY INTO STUDENT LEARNING

PREMODULE ASSESSMENT

With Eureka Math2, the learning begins by making sure students are prepared with the foundational knowledge needed to take on new learning. Eureka Math2 Equip™ provides digital premodule assessment, assessment reporting, and an acceleration plan of action to support students so everyone can access grade-level content.

FORMATIVE ASSESSMENT

While all assessments in Eureka Math2 are formative in nature, a strategic array of progress-monitoring tools ensures students are on track and gives teachers data to make real-time course corrections to support gradelevel proficiency.

• Observational Assessment Recording Sheets are short, qualitative checklists that capture student progress.

• Exit Tickets at the end of daily lessons provide a window into student understanding to inform instructional decisions.

• Topic Tickets, for Grades 1–2, take the place of an Exit Ticket at the end of a Topic.

SUMMATIVE ASSESSMENT

Educators can measure proficiency with major concepts, skills, and applications against standards over time with Eureka Math2 summative assessments.

• Topic Quizzes, for Grades 3–Algebra I, assess a student’s understanding of the full Topic, or a week of lessons.

• Performance Tasks engage students in rich problem-solving experiences to demonstrate their ability to synthesize understanding of multiple content standards.

• Module Assessments assess student proficiency with the major concepts, skills, and applications at the end of each module.

• Benchmark Assessments assess student proficiency with math skills and concepts from the two previous modules, and with select review skills reflecting the major work of the grade.

•

•

•

Differentiation: Fuel Growth and Accelerate Learning

With Math Catalyst™ multi-leveled intervention and acceleration resources, teachers can activate a classroom full of energy, sparking advantages for all levels of students to succeed. Through extension, spiral review, practice, or explicit and systematic direct intervention instruction, students accelerate forward.

Math Catalyst includes content across seven strands to reinforce K–5 standards. It can also support students in Grades 6+ who need remediation with essential K–5 concepts. Each strand is composed of a progression of concepts, and each concept includes a series of components, shown below, that can be used in small group direct instruction as well as at stations.

Concept Guide

Includes preparation materials, student misconceptions, language supports, and family support

Progress Check

Measures student proficiency to guide instructional decisions

Concept Mini Lessons

Made up of 76 Concepts across almost 300 Mini Lessons for small group instruction

Practice

Provides spaced retrieval and repetition and spiral review opportunities

Application

Provides opportunities for extension and the building of fluency and automaticity

Strand

Early Numeracy

Place Value

Addition

Subtraction

Multiplication

Division

Fractions as Numbers

Address on-level practice, remediation, and advanced learning

Address learning gaps in any grade

Empowering Teachers

Eureka Math2 simplifies implementation for both new and experienced educators through embedded margin notes and just-in-time strategies to support all learners. Educators gain deeper content knowledge and have access to robust pedagogical tools, empowering them to meet the demands of today’s classroom with confidence.

UNLOCK THE POWER OF PROFESSIONAL LEARNING

Whether it’s through virtual learning sessions, onsite professional development, or personalized coaching, a team of experienced educators and content specialists from Great Minds will work with you to develop a multiyear professional learning plan. These plans are built to support teachers and curriculum leaders in achieving their goals and setting up students for mathematical success. Because we know that when teachers feel confident, students thrive.

ACCESS DIGITAL PROFESSIONAL DEVELOPMENT ANYTIME

With over 150 videos designed to support teachers, the Great Minds digital platform has everything a teacher needs to feel supported during their math instruction.

2.7 MILLION STUDENTS

We know that every child is capable of greatness. Eureka Math2 empowers teachers to create exponentially greater aha moments for all students.

To learn more, visit greatminds.org/math/eurekamathsquared