LEERWERKBOEK
Meetkunde
Björn Carreyn
Filip Geeurickx
Roger Van Nieuwenhuyze
CARTOONS
Dave Vanroye
Hoe gebruik je VBTL ?
Dit boek bevat zes hoofdstukken vol meetkunde. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting. Bij de inhoudstafel van elk hoofdstuk kun je ook een QR-code vinden. Via die codes kun je extra filmpjes met uitleg bekijken.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt. Wiskunde kent veel links met andere vakken We tonen zo’n link in een paarsgekleurd kadertje.
1 2 *
Na de samenvatting vind je een reeks oefeningen Bij oefeningen die extra uitdagend zijn, zie je een sterretje naast het nummer.
Bij sommige oefeningen moet je verder denken dan de net geziene leerstof. Je maakt dan gebruik van heuristieken. Deze oefeningen herken je aan de wiskunderugzak
ICT is een ideaal hulpmiddel. Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.
INKIJKEXEMPLAARDIEKEURE
Vaardigheden
Na elk hoofdstuk wordt een wiskundige vaardigheid in de kijker gezet. Ook in het portfolioschriftje dat bij dit boek hoort, kun je vaardigheden inoefenen.
Wat moet je kennen en kunnen ?
Na de vaardigheden zie je een handig overzicht van wat je moet kennen en kunnen na het geziene hoofdstuk. Kleur de eerste kolom smileys als je de leerstof herhaalde voor een grote toets. Kleur de laatste kolom als je de leerstof beheerst voor je examen.
Herhalingsoefeningen
Wanneer je wiskunde studeert, maak je uiteraard heel wat oefeningen opnieuw en maak je oefeningen die je in de klas niet maakte.
Elk hoofdstuk sluit af met drie pagina’s herhalingsoefeningen
Een ideale test voor jezelf om te zien of je de leerstof beheerst.
Welkom in de wondere wereld van de wiskunde !
We hebben ons best gedaan om het vak wiskunde niet voor te stellen als een saaie, droge materie, maar wel als een boeiende en levende wetenschap waar je ook in werkelijkheid mee geconfronteerd wordt.
Wie had immers gedacht dat deze prachtige tuin vol zit met meetkundige transformaties en symmetrie?
Wandel met ons mee door de mooie en erg logisch opgebouwde wereld van meetkundige figuren.
INKIJKEXEMPLAARDIEKEURE
Inhoud
INKIJKEXEMPLAARDIEKEURE
Meetkunde
INKIJKEXEMPLAARDIEKEURE
1
Transformaties
1.1 Even observeren 9
1.2 Spiegeling om een as 10
1.3 Translatie over een vector 19
1.4 Rotatie rond een centrum over een hoek 29
1.5 Symmetrie 43
1.6 Eigenschappen van transformaties 52
1.7 Verband tussen coördinaten in een assenstelsel en transformaties 63
70
2
Hoeken
2.1 Even observeren 77
2.2 Soorten hoeken 78
2.3 Hoeken bij evenwijdigen en een snijlijn 90
2.4 Som van de hoeken in een veelhoek 104 Extra’s 118
3
Congruentie
3.1 Even observeren 127
3.2 Congruentie 128
3.3 Verantwoorden van constructies 154
4
Driehoeken
4.1 Eigenschappen onderzoeken 179
4.2 De driehoeksongelijkheid 195
202
5
Vierhoeken
5.1 Eigenschappen onderzoeken 209
5.2 Vierhoeken construeren en classificeren 233
242
6
Ruimtemeetkunde
6.1 Ruimtefiguren herkennen
6.2 Volume van ruimtefiguren
Transformaties
Wolkenkrabbers met een twist ? Je zou het niet meteen verwachten, maar je vindt er in heel wat landen wel terug : van Zweden tot China, van Rusland tot Panama …
1 INKIJKEXEMPLAARDIEKEURE
De toren op deze foto heet de Cayan Tower en die vind je in Dubai. Hij is precies 330 meter hoog en telt 73 verdiepingen. Het bovenvlak is precies 90 graden gedraaid ten opzichte van het grondvlak.
In Zweden en Rusland vind je gebouwen die eenzelfde hoek beschrijven, maar sommige wolkenkrabbers draaien soms 120 ° om hun as, of meer zelfs …
Draaien is een van de transformaties die je in dit hoofdstuk zult bestuderen.
Transformaties
1.1 Even observeren 9
1.2 Spiegeling om een as
1 Spiegeling van een punt om een as 10
2 Spiegeling van een driehoek om een as 11
3 Vlakke figuren spiegelen om een as met ICT 12
4 Samenvatting 13
5 Oefeningen 14
1.3 Translatie over een vector
1
2 Gelijke vectoren
3 Translatie van een punt over een vector
4 Translatie van een driehoek over een vector 22
5 Vlakke figuren verschuiven over een vector met ICT 23
6 Samenvatting 23
7 Oefeningen 24
1.4 Rotatie rond een centrum over een hoek
1 Georiënteerde hoeken 29
2 Rotatie van een punt over een hoek 30
3 Rotatie van een driehoek over een hoek 31
4 Vlakke figuren roteren over een hoek met ICT 32
5 Spiegeling om een punt 33
6 Samenvatting 34 7 Oefeningen 35
1.5 Symmetrie
1 Spiegelsymmetrie om een as 43
2 Spiegelsymmetrie om een punt 44
3 Draaisymmetrie om een punt 44
4 Samenvatting 45 5 Oefeningen 46
1.6 Eigenschappen van transformaties
1 Transformaties van het vlak 52
2 Op zoek naar eigenschappen 54
3 Samenvatting 56 4 Oefeningen 57
1.7 Verband tussen coördinaten in een assenstelsel en transformaties
1 Samenhang tussen spiegelingen en coördinaten van punten 63
2 Samenhang tussen translaties en coördinaten van punten 65
3 Samenhang tussen puntspiegeling en coördinaten van punten 66
4 Samenvatting 66 5 Oefeningen 67
Extra’s
Vaardigheden : een transformatie is niet altijd een isometrie 70
Wat moet je kennen en kunnen ? 71
Herhalingsoefeningen 72
Bekijk de instructievideo’s
Even observeren
Hier vind je een collage van een aantal mooie foto’s.
Bekijk de foto’s en bespreek wat er te zien is.
INKIJKEXEMPLAARDIEKEURE
1.2 Spiegeling om een as
1 Spiegeling van een punt om een as
A is het punt dat we willen spiegelen.
a noemen we de spiegelas, of kortweg de as.
Teken door het punt A de loodlijn l op de rechte a
M is het snijpunt van l met a .
Bepaal het punt A′ zodat | AM | = | MA′ |
Het punt A′ is het spiegelbeeld van het punt A om de as a .
In symbolen : A′ = sa ( A)
Merk op :
– Als het punt A′ het spiegelbeeld is van het punt A om de as a , dan is a de middelloodlijn van [AA′].
– Ligt het punt A dat je wilt spiegelen op de spiegelas zelf, dan heeft A zichzelf als spiegelbeeld.
We noemen A een dekpunt.
In symbolen : ∀ A ∈ a : sa ( A) = A
2 Spiegeling van een driehoek om een as
∆ ABC is de driehoek die we willen spiegelen.
a is de spiegelas.
INKIJKEXEMPLAARDIEKEURE
Om een driehoek te spiegelen om een as is het voldoende dat je het spiegelbeeld van elk hoekpunt van die driehoek bepaalt.
Je krijgt het spiegelbeeld door de spiegelpunten met elkaar te verbinden.
D A′B′C′ is het spiegelbeeld van ∆ ABC om de as a
In symbolen:
′B′C′ = sa ( ∆ ABC)
3 Vlakke figuren spiegelen om een as met ICT
a Een vierhoek spiegelen
Stappenplan om dit met ICT te tekenen:
– Teken een vierhoek ABCD.
– Teken een rechte EF.
Spiegel de vierhoek om de as EF door op het derde laatste icoontje te kiezen voor lijnspiegeling.
Klik nu eerst op de getekende vierhoek en dan op de rechte EF.
Teken de rechten AA′, BB′ , …
–
INKIJKEXEMPLAARDIEKEURE
Duid de snijpunten aan van die rechten met de rechte EF.
– Duid alle hoeken aan die de rechten maken met de rechte EF.
Zorg ervoor dat je het symbool voor rechte hoek gebruikt. Klik daarvoor eerst op de selecteerknop en klik dan met de rechtermuisknop in het tekenvenster. Kies onderaan voor tekenvenster en selecteer dan helemaal onderaan (bij stijl voor rechte hoek) het gepaste symbool.
Teken de nodige lijnstukken en selecteer ze in het algebravenster. Klik erop met de rechtermuisknop, ga naar instellingen en dan naar stijl. Kies een gepaste markering.
Versleep een van de hoekpunten van vierhoek ABCD en observeer wat er gebeurt.
Blijven de rechten AA′, BB′, … loodrecht staan op de rechte EF ?
Blijft de afstand van A tot de as EF dezelfde als de afstand van A′ tot de as ?
Blijft dit ook geldig voor alle andere punten van de vierhoek ABCD ?
Je krijgt een nieuwe situatie door punten van de vierhoek of de vierhoek zelf te verslepen.
Merk op :
EF is de middelloodlijn van [AA′], [BB′], [CC′] en [DD′].
b Een cirkel en een regelmatige vijfhoek spiegelen
Werk dit uit met ICT.
INKIJKEXEMPLAARDIEKEURE
4 Samenvatting
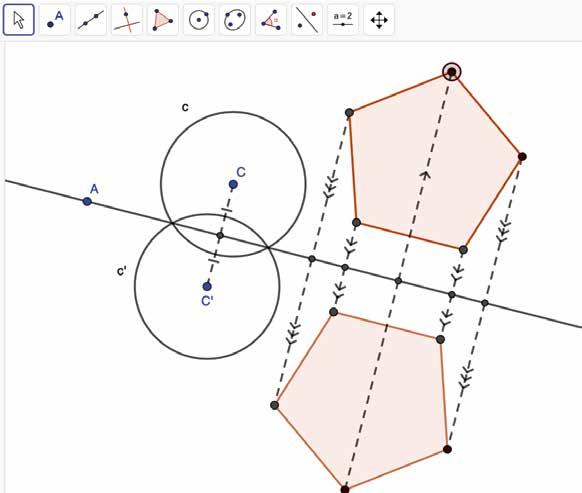
• Je kunt het verband leggen tussen een vlakke figuur en haar beeld onder een spiegeling om een as.
• Je kunt een vlakke figuur spiegelen om een as (met en zonder ICT).
• Je kunt sa ( A) = A′ lezen als A′ is het spiegelbeeld van A om de as a
5 Oefeningen
In spiegeling herken je het woord spiegel. In welke beroepen maken mensen gebruik van een spiegel en waarom gebruiken ze dat voorwerp ?
Teken telkens het spiegelbeeld van de aangeduide punten om de as s
Teken de beelden van de aangeduide punten door ze te spiegelen om de as a
Spiegel de onderstaande veelhoeken om de as s a c s C B A s J I H
s
Wiskundetaal : hoe lees je volgende notaties ? a sa ( P) b B = sa ( A) c sm ( D XYZ) = D X′Y′Z′
Schrijf in symbolen.
a D A′B′C′ is het spiegelbeeld van D ABC om de as a .
b B′ is het spiegelbeeld van B om de as DE.
c Spiegel het punt Q om de as RT.
Gegeven : zie figuur onderaan
Gevraagd :
a Hoe lees je volgende notaties ?
s x ( A) = C A = s x ( C)
b Vul in.
s x ( A) = s x ( C) = s y ( D) =
s y ( B) = s y ( C) = s x ( B) =
c Teken K = sx ( E)
Teken L = sy ( E)
Welke figuur vormt KLCA ?
′, B′, C′ en D′ zijn de beelden van A, B, C en D door de spiegeling om x . Teken A, B, C en D.
Gegeven : A′ = sa ( A) het punt B
Gevraagd : zoek sa ( B) = B′
Teken de spiegelas a als X′ = sa ( X) en Y′ = sa ( Y)
Gegeven : zie figuur
Gevraagd : vul aan
Tekenopdrachten met ICT.
a Teken een rechthoek ABCD. Teken een diagonaal en spiegel de rechthoek om deze diagonaal.
Kleur het resultaat groen in.
b Teken een parallellogram ABCD. Teken een diagonaal en spiegel het parallellogram om deze diagonaal.
Kleur het resultaat oranje in.
c Teken een stomphoekige driehoek ABC met de stompe hoek in A.
Spiegel deze driehoek om BC.
Hoe noem je de vierhoek ABA’C ?
d Ontwerp een figuur en een spiegelas, zodat het spiegelbeeld van deze figuur om de getekende as met de oorspronkelijke figuur samenvalt.
e Spiegel een vierkant ABCD om de dragers van zijn zijden. Je voert dus vier spiegelingen uit.
–
Kleur elk bekomen spiegelbeeld anders in.
– Focus op de verschillende spiegelbeelden van het punt A.
Welke figuur vormen deze ?
–
Wat kan je concluderen als je de oppervlakte van deze figuur vergelijkt met de oppervlakte van het oorspronkelijke vierkant ?
f De bissectrice van een hoek is de rechte die deze hoek in twee gelijke hoeken verdeelt.
Als je in het hoekpunt op deze bissectrice de loodlijn tekent, dan bekom je de buitenbissectrice.
Teken in een driehoek ABC de binnen- en buitenbissectrice van A.
Spiegel de driehoek om elk van deze bissectrices.
Met welke beeldpunten kan je een parallellogram vormen?
Kleur deze parallellogram geel in.
De gewone dobbelsteen D staat voor een spiegelhoek.
Welke spiegelbeelden zijn zeker fout ?
(A) alleen A (B) alleen B (C) alleen C (D) alleen A en B (E) alleen B en C
JWO 2019 eerste ronde, vraag 6 © Vlaamse Wiskunde Olympiade vzw
Zoë schrijft de afkorting voor “zie ommezijde” op een doorzichtig blad papier. Door het blad in verschillende richtingen om te keren, kan ze vier van de onderstaande figuren zien. Welke figuur kan Zoë niet zien?
JWO 2024, eerste ronde, probleem 9 © Vlaamse Wiskunde Olympiade vzw
1.3 Translatie over een vector
1 Vector
Een voetballer wil een bal over de grond trappen. Hij heeft hier natuurlijk veel mogelijkheden voor. De andere spelers denken hierover na :
– Welke richting zal hij de bal geven ?
In welke zin (= oriëntatie) zal hij de bal trappen ?
– Hoe ver zal hij de bal trappen ?
INKIJKEXEMPLAARDIEKEURE
De bal vertrekt vanuit A en gaat naar het punt B. Als de tweede speler de bal terugspeelt, dan gaat de bal van punt B naar punt A.
Als we de oriëntatie hebben aangeduid, hebben we een vector (of een georiënteerd lijnstuk). We hebben dan (met een pijlpunt) een zin aangeduid. Een van de grenspunten is nu het beginpunt, het andere het eindpunt.
Een vector is een lijnstuk waarop een doorloopzin (oriëntatie) is aangeduid.
2 Gelijke vectoren
Bekijk aandachtig de drie hiernaast getekende vectoren −→ AB, −→ CD en −→ EF .
Wat valt je op?
Evenwijdig ? AB ⫽ CD ⫽ EF
Als rechten evenwijdig zijn, bepalen ze dezelfde richting.
Even lang ? | AB | = | CD | = | EF |
Oriëntatie? De zin van −→ AB, −→ CD en −→ EF is dezelfde.
Als vectoren evenwijdig zijn, even lang zijn en dezelfde oriëntatie hebben, dan zijn ze gelijk.
Conclusie : −→ AB = −→ CD = −→ EF
gelijke vectoren
Gelijke vectoren zijn vectoren die dezelfde richting, lengte en zin hebben.
Een vector bepaalt een translatie
We spreken dan van de translatie bepaald door −→ AB en kunnen dit noteren als t −→ AB Die translatie is net dezelfde als de translatie bepaald door −→ CD ( t −→ CD ) of de translatie t −→ EF (zie tekening bovenaan).
In onderstaande voorbeelden bepalen −→ XY en −→ PQ verschillende translaties.
Voorbeeld 1: Voorbeeld 2: Voorbeeld 3:
De zin is verschillend. De lengte is verschillend. XY en PQ zijn niet evenwijdig, de richting is verschillend.
3 Translatie van een punt over een vector
Na de spiegeling bestuderen we nu een tweede transformatie van het vlak: de translatie (t ) over een vector.
Hoe teken je het schuifbeeld van het punt A over vector −→ CD ?
A is het punt dat we willen verschuiven.
−→ CD is de gegeven vector.
INKIJKEXEMPLAARDIEKEURE
Teken door het punt A een evenwijdige rechte met CD.
De richting is nu in orde.
Bepaal nu de zin van de pijl.
Zoek een punt A′ zodat | CD | = | AA′|.
De zin en de lengte zijn nu ook in orde.
A′ is het schuifbeeld van A.
Het punt A′ is het schuifbeeld van het punt A door de translatie bepaald door vector −→ CD
In symbolen :
A′ = t −→ CD( A)
Merk op : Een bijzondere translatie is t −→ AA = t −→ BB = .... Elk punt van het vlak wordt afgebeeld op zichzelf.
We noemen dit de identieke transformatie.
Translatie
Het woord ‘translatie’ is afgeleid van het Latijnse ‘translatio’. Dat betekent vertaling, omzetting of overdraging. De meetkundige figuur wordt eigenlijk ‘overgedragen’ naar een andere plaats.
Denk ook aan het Engelse ‘translation’, wat staat voor vertaling. Ook in de economie wordt het woord gebruikt om iemands rechtsgebied te verleggen.
4 Translatie van een driehoek over een vector
Voorbeeld :
D ABC is de driehoek die we willen verschuiven.
De translatie wordt bepaald door vector −→ EF
Om een driehoek te verschuiven volgens vector −→ EF is het voldoende dat je het schuifbeeld van elk hoekpunt van die driehoek bepaalt.
Je krijgt het schuifbeeld van D ABC door de schuifbeelden A′, B′ en C′ met elkaar te verbinden.
D A′B′C′ is het schuifbeeld van D ABC over vector −→ EF
In symbolen :
5 Vlakke figuren verschuiven over een vector met ICT
a Een vierhoek verschuiven
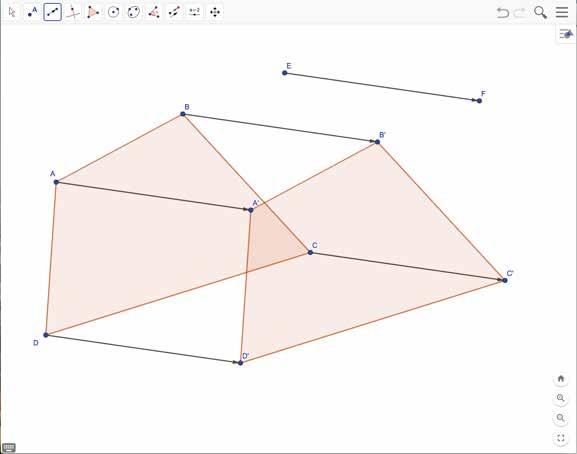
b Een cirkel en een regelmatige zeshoek verschuiven
Werk dit uit met ICT.
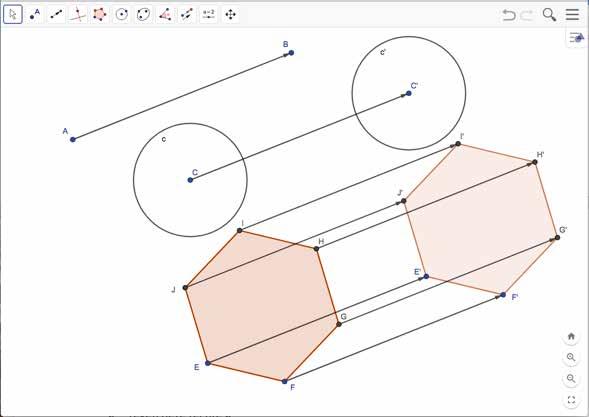
Stappenplan om dit met ICT te tekenen :
– Teken een vierhoek ABCD.
– Teken een vector −→ EF.
– Klik op het derde laatste icoontje en kies voor verschuiving door vector. Klik nu eerst op de getekende vierhoek en dan op de vector −→ EF
– Teken eveneens de vectoren −→ AA , −→ BB , −→ CC en −→ DD
INKIJKEXEMPLAARDIEKEURE
6 Samenvatting
• Je weet wat een vector is en wanneer vectoren gelijk zijn.
• Je kent het verband tussen een vlakke figuur en haar beeld onder een translatie over een vector.
• Je kunt van een vlakke figuur haar beeld bepalen onder een translatie over een vector (met en zonder ICT).
• Je kunt A′ = t −→ CD (A) lezen als A′ is het schuifbeeld van A door de translatie over een vector −→ CD.
7 Oefeningen
Duid in deze strook behangpapier drie verschillende vectoren t , u en v aan. Teken voor elk van deze vectoren een gelijke vector.
Teken telkens het schuifbeeld van de punten A, B en C door de translatie bepaald door vector −→ XY
Zoek de beelden van A, B en C door de translatie bepaald door vector
Is t −→ AA = t −→ BB ? Verklaar. a b c
Teken het beeld van de onderstaande veelhoeken door de translatie bepaald door vector −→ XY
c
Wiskundetaal : hoe lees je volgende notaties ?
a t −→ KT (C)
b T = t −→ AB (L)
INKIJKEXEMPLAARDIEKEURE
c t −→ NF (R)= S
Schrijf in symbolen.
a D′ is het schuifbeeld van D over vector −→ EF
b DR′T′V′ is het schuifbeeld van DRTV over vector −→ AB
c Verschuif F over vector −→ KL .
Zoek telkens het schuifbeeld en vorm met de verkregen letters een wiskundig begrip.
a t −→ KT (C)=
b t −→ IO (A)=
c t −→ RE (E)=
d t −→ MJ (O)=
e t −→ MZ (E)=
f t −→ BC (Z)=
g t −→ FZ (D)=
h t −→ FN (A)=
i t −→ AA (E)=
j t −→ NA (R)=
k t −→ VL (Q)= Het woord is :
Gegeven : zie figuur
Gevraagd : vul aan
a t −→ AB (E)= h t −→ BE (∆BFD)=
b t −→ AB (G)= i t −→ HE ( )= C
c t −→ FC (H)= j t −→ CB ( )= D
d t GA (I)= k t IE ( )= y
e t −→ BC ( x )= l t (p )= q
f t −→ AI (p )= m t (HF)= DB
g t −→ HI ([BD])= n t (G)= F
a Teken in het groen een vector die vierkant ABFE afbeeldt op vierkant FGKJ.
b Teken in het rood een vector die vierkant GHLK afbeeldt op vierkant BCGF.
c Wat kan je besluiten in verband met je twee getekende vectoren?
Bepaal een translatie t zodat t ( c ) = c ′
Tekenopdrachten met ICT.
a Teken een vierkant ABCD en een willekeurige vector −→ EF.
Teken het beeld van dit vierkant onder de translatie over −→ EF
Kleur het schuifbeeld blauw in.
b Teken een stomphoekige driehoek ABC met stompe hoek in A.
Teken het beeld van deze driehoek onder de translatie over de vector −→ BC.
Hoeveel keer past de oorspronkelijke driehoek in figuur ABC′A′?
c Teken een rechthoek ABCD.
Teken het beeld van deze rechthoek onder de translatie over de vector −→ DA
Kleur het resultaat groen in.
d Teken een parallellogram ABCD.
Teken het beeld van dit parallellogram onder de translatie over de vector −→ AC .
Kleur het resultaat oranje in.
e Teken een ruit ABCD. Kleur ze rood in. Je zal deze ruit nu drie keer verschuiven en telkens rood inkleuren.
– Teken het beeld van de ruit ABCD onder de translatie over de vector −→ AB –
Teken het beeld van de ruit ABCD onder de translatie over de vector −→ AC
– Teken het beeld van de ruit ABCD onder de translatie over de vector −→ AD.
Wat kan je besluiten over de grootste vierhoek die zo ontstaat?
Bepaal in een regelmatige achthoek een aantal koppels die behoren tot eenzelfde translatie. Oorsprong en uiteinde moeten hoekpunten zijn van de achthoek.
Hoeveel verschillende translaties zijn hier mogelijk ?
1.4 Rotatie rond een centrum over een hoek
1 Georiënteerde hoeken
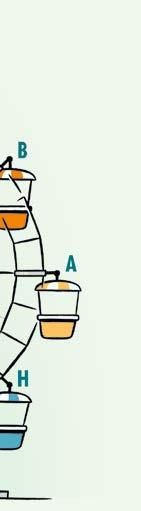
Lien zit op het reuzenrad. Het punt waarrond het rad draait, noemen we O.
INKIJKEXEMPLAARDIEKEURE
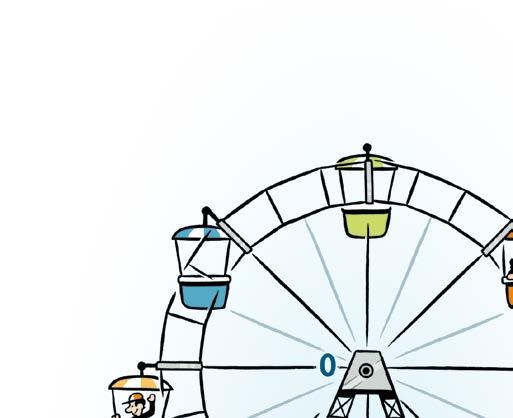
O wordt het centrum van de rotatie (of draaiing) genoemd.
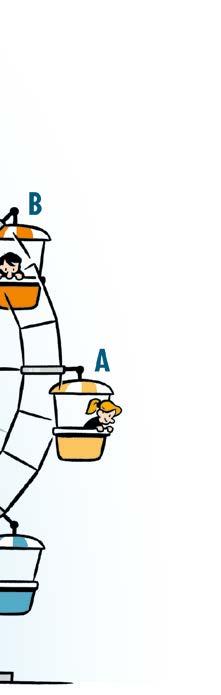
De hoek waarover gedraaid wordt, noemen we de draaiingshoek. Maar opgelet ! Je kunt het rad in wijzerzin of in tegenwijzerzin laten draaien. De hoek gevormd door de benen [ OA en [ OB kunnen we dus op twee manieren doorlopen.
IN TEGENWIJZERZIN IN WIJZERZIN
[ OA: beginbeen [ OB: eindbeen
afspraak: tegenwijzerzin = positieve zin
[ OB: beginbeen [ OA: eindbeen
afspraak : wijzerzin = negatieve zin de georiënteerde hoek AOB is 45° de georiënteerde hoek BOA is – 45°
georiënteerde hoek
Een georiënteerde hoek is een hoek waarop een oriëntatie is aangeduid.
Merk op:
Een georiënteerde hoek wordt bepaald door het hoekpunt, de oriëntatie en de hoekgrootte.
2 Rotatie van een punt over een hoek
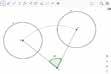
Als derde transformatie van het vlak bestuderen we de rotatie rond een centrum over een hoek. Hoe teken je het draaibeeld van het punt A door de rotatie rond het punt O over een hoek van 60° ?
A is het punt dat we willen draaien (of roteren).
O is het punt waarrond we draaien: we noemen dit het centrum van de rotatie.
De draaiingshoek is 60°. Dat is dus in tegenwijzerzin.
INKIJKEXEMPLAARDIEKEURE
Zet je passerpunt in het punt O en teken in tegenwijzerzin een cirkelboog door A.
Teken een hoek van 60° met als hoekpunt O en als eerste been [ OA.
Het snijpunt van het tweede been met de cirkelboog noem je A′
Zo is de hoek AOA′ = 60°.
Het punt A′ is het draaibeeld van het punt A door rotatie rond het punt O over een hoek van 60°.
In symbolen : A′ = r ( O, 60°) ( A)
Rotatie
Het woord ‘rotatie’ is afgeleid van het Latijnse ‘rotare’, wat letterlijk draaien of omwentelen betekent.
Ook in de sterrenkunde wordt dit woord gebruikt als eigenschap van de hemellichamen. Zo verloopt de rotatie van een hemellichaam positief als de omwenteling rond de as in dezelfde zin gebeurt als zijn beweging rond de zon.
Bij de aarde en de maan is er sprake van een ‘gebonden rotatie’. Dat wil zeggen dat de omlooptijd en de rotatietijd van de maan gelijk zijn.
Onze getijden (eb en vloed, door de maan opgewekt) zorgen voor een versnelling van de rotatietijd van de aarde.
3 Rotatie van een driehoek over een hoek
D ABC is de driehoek die we willen roteren rond het punt O over een hoek van –100°.
Om een driehoek te roteren over een georiënteerde hoek is het voldoende dat je het draaibeeld zoekt van elk hoekpunt.
Je krijgt het draaibeeld van D ABC door de draaibeelden A′, B′ en C′ met elkaar te verbinden.
′ C′
D A′B′C′ is het draaibeeld van D ABC door de rotatie rond het punt O over een hoek van –100°.
In symbolen :
D A′B′C′ = r ( O, –100°)( D ABC)
4 Vlakke figuren roteren over een hoek met ICT
a Een vierhoek roteren
Teken een vierhoek ABCD en een punt O en roteer de vierhoek in tegenwijzerzin rond O over een hoek van 95 °.
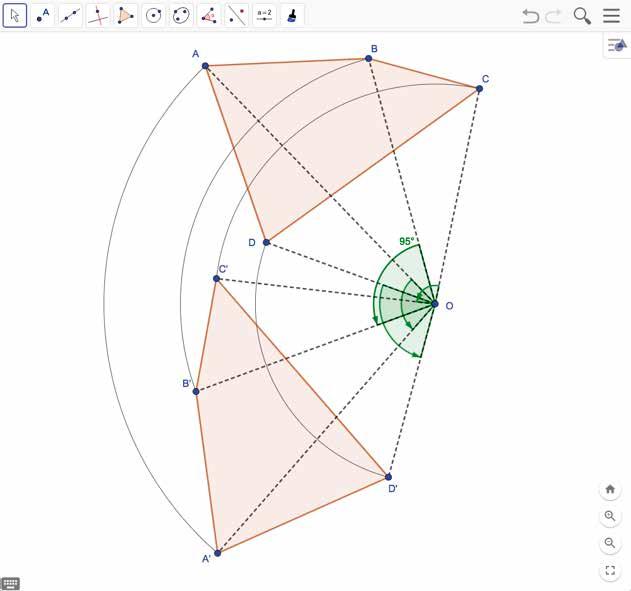
b Een cirkel roteren over een bepaalde hoek
Stappenplan om dit met ICT te tekenen:
– Teken een vierhoek ABCD en een punt O.
– Klik op het derde laatste icoontje en kies voor roteer rond punt. Klik eerst op de getekende vierhoek en dan op O.
– Kies dan bij het scherm dat zich opent voor tegenwijzerzin en als grootte van de hoek vul je 95 ° in.
– Teken alle stippellijnen.
– Teken alle cirkelbogen (gebruik het icoontje cirkelboog).
– Duid alle hoeken aan.
Merk op :
Een vierhoek roteren over een hoek van 95 ° in tegenwijzerzin komt dus neer op een vierhoek roteren over een hoek van +95 °.
INKIJKEXEMPLAARDIEKEURE
Teken een cirkel c en roteer die cirkel in wijzerzin rond O over een hoek van 75 °.
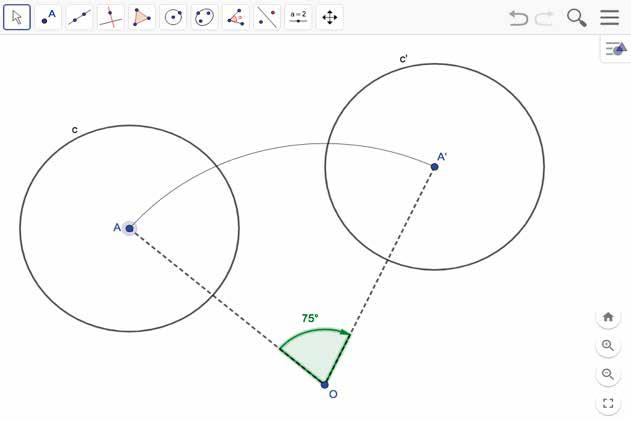
Merk op :
Een cirkel roteren over een hoek van 75 ° in wijzerzin komt dus neer op een cirkel roteren over een hoek van –75 °.
5 Spiegeling om een punt
Roteer een punt A rond het centrum O over een hoek van 180 °.
INKIJKEXEMPLAARDIEKEURE
′
Merk op:
O is het midden van het lijnstuk [ AA′].
– Een rotatie met draaiingshoek 180° is hetzelfde als een rotatie met draaiingshoek –180°.
Een dergelijke rotatie noemen we ook een puntspiegeling met centrum O.
puntspiegeling
Een puntspiegeling met centrum O is een rotatie over 180° rond O.
Het is niet nodig om een puntspiegeling met een passer uit te voeren. Je kunt het sneller met een geodriehoek.
Voorbeeld 1 : spiegelen van een punt om een punt
O is het centrum van de puntspiegeling.
A is het punt dat we willen puntspiegelen.
Teken de rechte AO.
Bepaal een punt A′ zodat O het midden is van [ AA′]
A′ is het beeld van het punt A door de puntspiegeling om O.
In symbolen :
Voorbeeld 2 : spiegeling van een driehoek om een punt
Teken met ICT een driehoek ABC en een punt O. Spiegel de driehoek om het punt O.
INKIJKEXEMPLAARDIEKEURE
6 Samenvatting
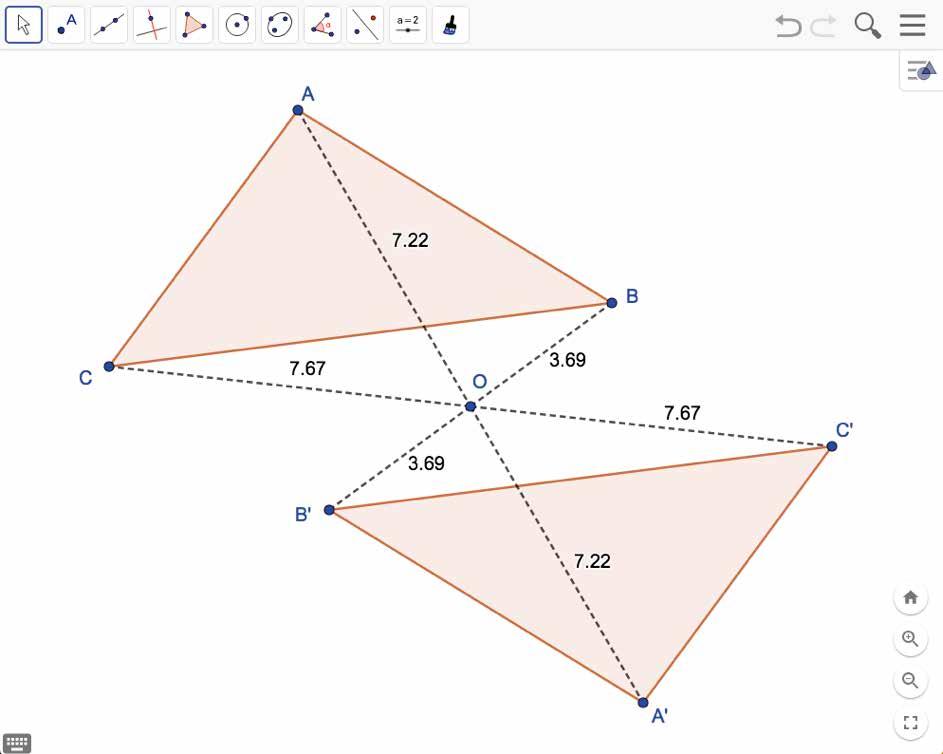
• Je weet dat een georiënteerde hoek een hoek is waarop een oriëntatie werd aangebracht.
• Je kan het verband leggen tussen een vlakke figuur en haar beeld onder een rotatie rond een centrum over een hoek.
• Je kunt een vlakke figuur roteren rond een centrum over een bepaalde hoek (met en zonder ICT).
• Je kunt een vlakke figuur spiegelen om een punt (met en zonder ICT).
• Je kunt A′ = r ( O, α)( A) lezen als A′ is het draaibeeld van A door rotatie rond het centrum O over een hoek α
7 Oefeningen
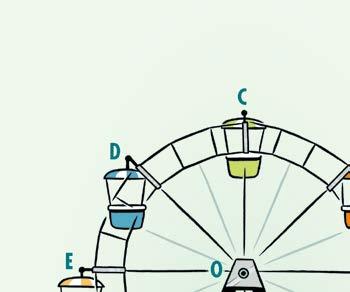
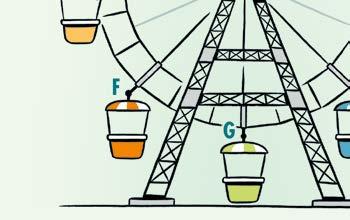
Vul de zinnen aan.
a C is het draaibeeld van A als je roteert om over
b H is het draaibeeld van D als je roteert om over
c F is het draaibeeld van C als je roteert om over
d E is het draaibeeld van H als je roteert om over
e B is het draaibeeld van B als je roteert om over
Teken telkens het beeld van een punt A onder de rotatie rond het punt O …
a … over een hoek van –30°.
c … over een hoek van 70°.
b … over een hoek van 140°. d … over een hoek van –90°.
Teken het beeld van de meetkundige figuur onder de rotatie rond O over een hoek α
a α = 160°
INKIJKEXEMPLAARDIEKEURE
b α = 75°
4 5 6
Wiskundetaal : hoe lees je volgende notaties ?
a r ( T, 70°)
b A′ = r ( D, –70°)( A)
INKIJKEXEMPLAARDIEKEURE
c ∆D′E′F′ = r ( O, 170°)( DDEF)
Schrijf in symbolen.
a Roteer K over een hoek van 70 ° om O.
b B′ is het draaibeeld van B door een rotatie om O over –120 °.
c D J′K′L′ is het draaibeeld van D JKL door een rotatie om L over 35 °.
Iedereen die af en toe een spelletje speelt, kent wel Tetris of Blokken. In dit spel is het de bedoeling lijnen te vormen door de verschillende blokjes naar beneden te brengen. Dit spel zit vol rotaties (over 90 °, 180 ° of –90 °) en verschuivingen (naar links, rechts en beneden, maar jammer genoeg niet naar boven). Hieronder zie je de verschillende blokjes. Schets onder elk blokje wat je krijgt als je het blokje roteert over de gevraagde hoek.
Anke, Barbara, Ciska en Dora staan aan het ‘Rad van fortuin’ en mogen elk twee keer draaien. Ze winnen telkens het bedrag dat voor hun neus stopt. Daarna wordt het rad weer in deze positie teruggeplaatst. Wie gaat met het hoogste bedrag naar huis ?
Gegeven : zie figuur Gevraagd : vul aan
a r ( O, 30°)( B) =
b r ( O, 45°)( D) =
c r ( O, –60°)( A) =
d r ( O, 75°)([ TI]) =
e r ( K, 180°)( A) =
f r ( O, –90°)( ∆JCU) =
g r ( O, 90°)( ) = H
h r ( O, –60°)( ) = B
rotatiebedrag
Anke
Barbara
Ciska
Dora
r( O, –100°)
r( O, –170°)
r( O, –380°)
r( O, –145°)
r( O, –375°)
r( O, –280°)
r( O,–440°)
r( O,–350°)
i r ( O, –75°)( ) = N l r ( O, )( L) = P
j r ( O, )( J) = G
k r ( O, )( U) = S
r ( , )( O) = F
( , )( K) = K
Puntspiegel de punten om O.
Teken het beeld van de gegeven figuur onder een spiegeling om het punt M.
Wiskundetaal: hoe lees je de volgende notaties ?
A′ = sO( A) . Zoek B′
Gegeven : zie figuur
Gevraagd : vul aan
a s E( B) = h s E( DCFE) =
b s D( G) = i s F( ) = C
c s E( C) = j s H( ) = I
d s B( y ) = __________ k s E( ) = A
e s E( p ) = l s ( G) = A
f s E( BF) = __________ m s _______ ( FH) = BD
g s E([ IF) = n s ( p ) = r
Het woord ABBA wordt eerst geroteerd rond O over een hoek van 180°. Het resultaat wordt gespiegeld om de y -as. Wat is het resultaat?
Tekenopdrachten met ICT.
a Teken een rechthoek ABCD en een willekeurig punt O.
Roteer de rechthoek ABCD rond centrum O over een hoek van 60°.
b Teken een parallellogram ABCD. Teken de twee diagonalen.
Noem O het snijpunt van deze diagonalen.
Roteer het parallellogram rond O over een hoek van –90°.
c Teken een cirkel c met straal 5.
Kies een punt O op de cirkel.
Spiegel de cirkel om O.
d Teken een gelijkbenig trapezium ABCD.
Teken de twee diagonalen.
Noem O het snijpunt van deze diagonalen.
Spiegel het trapezium om O.
e Teken een gelijkzijdige driehoek ABC.
Kleur deze rood in.
Je zal nu twee rotaties uitvoeren en het resultaat telkens ook rood inkleuren. –
Draai ABC rond A over 120°.
– Draai ABC rond B over –120°.
Om een grote rode gelijkzijdige driehoek te bekomen moet nog één gebied ingevuld worden met een driehoek. Welke transformatie van het vlak kan je uitvoeren zodat je één grote rode gelijkzijdige driehoek bekomt?
f Breng de tekening hiernaast op het scherm.
Zoek sa ( D ABC)
Spiegel het bekomen beeld om O.
INKIJKEXEMPLAARDIEKEURE
g Teken het vierkant ABCD zodat co(A) = ( 1, 3), co(B) = ( 3, 3) en co(C) = ( 3, 1). Kleur de figuur groen.
Je zal deze figuur vier keer spiegelen om een punt en het resultaat telkens ook groen inkleuren.
– Spiegel ABCD om A.
– Spiegel ABCD om B.
– Spiegel ABCD om C.
– Spiegel ABCD om D.
Om een groot groen vierkant te krijgen moeten nog vier witte ruimtes opgevuld worden met een vierkant.
Welke transformaties van het vlak kan je uitvoeren zodat je één groot groen vierkant bekomt?
Gegeven : een regelmatige zeshoek ABCDEF
Gevraagd : vul aan
a sAD (B) =
b t −→ BC (F) =
c r(0,120 ◦ ) (F) =
d sO (D) =
e sFC (D) =
f t −→ BC (O) = j t −→ AO (∆ABO) =
g r(0,45 ◦ ) (O) = k s(0, 60 ◦ ) (∆ABO) =
h s (F) = Dl rO (∆ABO) =
i sO (∆ABO) = m t −→ DD (∆ABO) =
Vervang de gegeven transformaties door één. Welke?
a Roteer rond een willekeurig punt M over een hoek van 55°. Roteer daarna opnieuw rond M, maar nu over een hoek van 35°.
b Spiegel eerst om de oorsprong O. Spiegel daarna om de x -as.
c Spiegel om de y -as. Spiegel daarna om een rechte die evenwijdig is met de y -as.
d Puntspiegel om de oorsprong O. Roteer daarna rond O over een hoek van 40°.
e Roteer drie keer na elkaar rond eenzelfde punt P over 60°.
f Voer een translatie uit over vector
. Voer nadien een translatie uit over vector
1.5 Symmetrie
Sommige figuren hebben zichzelf als beeld als je ze spiegelt of draait. We spreken dan van symmetrie. In deze paragraaf bespreken we symmetrie bij vlakke figuren. In hoofdstuk 6 vind je de symmetrie bij ruimtefiguren.
1 Spiegelsymmetrie om een as
In de vlinder hierboven zit symmetrie. Als we de rechte a als spiegelas nemen, dan is het beeld van deze figuur de figuur zelf.
Een dergelijke rechte (spiegelas) noemen we een symmetrieas spiegelsymmetrisch om een as Een vlakke figuur is spiegelsymmetrisch om een as als ze zichzelf als beeld heeft bij een spiegeling om die as. Die rechte is een symmetrieas van de figuur.
Sommige veelhoeken hebben ook symmetrieassen. Dit zijn de symmetrieassen in de driehoeken en vierhoeken.
DRIEHOEKEN
ONGELIJKBENIGE
DRIEHOEK
Voorbeeld
Voorbeeld
Aantal
GELIJKBENIGE DRIEHOEK
GELIJKZIJDIGE
2 Spiegelsymmetrie om een punt
De figuur hiernaast kun je roteren rond het middelpunt over 180 °. Je krijgt dezelfde figuur.
Met andere woorden : je kunt de figuur puntspiegelen en het beeld bedekt perfect het origineel.
Het punt waar je om roteert, noemen we het symmetriemiddelpunt.
Een figuur kan maximaal één symmetriemiddelpunt hebben.
INKIJKEXEMPLAARDIEKEURE
spiegelsymmetrisch om een punt
Een vlakke figuur is spiegelsymmetrisch om een punt als ze zichzelf als beeld heeft bij een puntspiegeling om dat punt. Dit punt noemen we het symmetriemiddelpunt van de figuur.
3 Draaisymmetrie om een punt
Je kunt ook symmetrie hebben door te roteren.
Je kunt de molenwieken draaien zodat ze precies zichzelf als beeld hebben.
Die rotatie is een bijzondere rotatie. We noemen dit een eigendraaiing van de figuur. Niet alle figuren hebben eigendraaiingen. De rotatie over 0 ° wordt uitgesloten.
De figuur van de vijf molenwieken heeft volgende eigendraaiingen: r ( O, 72°), r ( O, 144°), r ( O, 216°) en r ( O, 288°)
draaisymmetrisch om een punt
Een vlakke figuur is draaisymmetrisch om een punt als ze zichzelf als beeld heeft bij een rotatie rond dat punt over een hoek verschillend van 0 °. Die rotatie noemen we een eigendraaiing van de figuur.
Merk op:
Als een figuur draaisymmetrisch is rond een punt over een hoek van 180 °, dan is ze ook spiegelsymmetrisch rond dat punt.
4 Samenvatting
• Je weet wanneer een vlakke figuur spiegelsymmetrisch is om een as. Een vlakke figuur is spiegelsymmetrisch om een as als ze zichzelf als beeld heeft bij een spiegeling om die as.
• Je weet wat een symmetrieas is.
• Je kunt de symmetrieassen aanduiden in een vlakke figuur.
• Je weet wanneer een vlakke figuur spiegelsymmetrisch is om een punt. Een vlakke figuur is spiegelsymmetrisch om een punt als ze zichzelf als beeld heeft bij een puntspiegeling rond dat punt.
• Je weet wat een symmetriemiddelpunt is.
• Je kunt het symmetriemiddelpunt aanduiden in een vlakke figuur.
• Je weet wanneer een vlakke figuur draaisymmetrisch is om een punt. Een vlakke figuur is draaisymmetrisch om een punt als ze zichzelf als beeld heeft bij een rotatie rond dat punt over een hoek verschillend van 0 °.
• Je weet wat een eigendraaiing is.
• Je kunt de eigendraaiingen bepalen van een vlakke figuur.
INKIJKEXEMPLAARDIEKEURE
Rorschach
De Zwitserse psychiater Hermann Rorschach gebruikte een reeks inktvlekken om een beeld te krijgen van de persoonlijkheid van zijn patiënten. De vlekken werden op een blad gebracht, waarna dat blad geplooid werd. Hierdoor ontstaan symmetrische figuren en kun je de plooi van het blad gelijkstellen met een spiegelas. De vlekken werden zeer doelbewust uitgekozen. Volgens sommigen was Hermann Rorschach de eerste die een verband legde tussen deze ‘vlekkenproef’ en de persoonlijkheid van zijn patiënten.
De ‘vlekkenproef’ bestaat uit tien gekleurde platen waarvan de onderzochte persoon moet zeggen wat hij in deze vlekken ziet.
Probeer jij ook eens te kijken ?
5 Oefeningen
Duid in onderstaande logo’s en borden alle symmetrieassen aan.
a d g j
b e h k
c f i l
Hieronder vind je zes kaarten uit een kaartspel.
Welke kaarten zijn spiegelsymmetrisch om een as ?
Welke kaarten zijn draaisymmetrisch om een punt ?
a b c d e
WALLABIE 2024 probleem 16 © Vlaamse Wiskunde Olympiade vzw 1 2 3 s
Een rooster bestaat uit 16 vierkanten, waarvan er 2 groen gekleurd zijn. Tarek wil nog 2 van die vierkanten groen kleuren zodat de rechte s een symmetrieas is van de figuur. Op hoeveel verschillende manieren kan hij dat doen? (A) 1 (B) 2 (C) 3 (D) 4 (E) 5
WISKUNDE & MAATSCHAPPIJ
Symmetrie in vlaggen. Hieronder vind je negen vlaggen. Zijn ze symmetrisch om een as en / of symmetrisch om een punt ?
symmetrisch om een as symmetrisch om een punt
symmetrisch om een as symmetrisch om een punt
INKIJKEXEMPLAARDIEKEURE
symmetrisch om een as symmetrisch om een punt
symmetrisch om een as symmetrisch om een punt
symmetrisch om een as symmetrisch om een punt
symmetrisch om een as symmetrisch om een punt
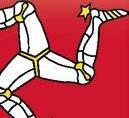
symmetrisch om een as symmetrisch om een punt
Bij de vlaggen van oefening 4 zijn er zeven draaisymmetrisch. Noteer van hun eigendraaiingen telkens de kleinste positieve hoek.
symmetrisch om een as symmetrisch om een punt
symmetrisch om een as symmetrisch om een punt
Zijn volgende figuren draaisymmetrisch ? Zo ja, noteer de eigendraaiingen. Gebruik steeds O als centrum.
e i
f j
INKIJKEXEMPLAARDIEKEURE
g k
h l
Waar of vals ? Als het antwoord vals is, teken dan een tegenvoorbeeld.
a Als een vierhoek twee symmetrieassen heeft, dan is het een ruit.
b Als een vierhoek één symmetrieas heeft, dan is het een gelijkbenig trapezium.
c Elk vierkant heeft vier symmetrieassen.
d Als een figuur twee symmetrieassen heeft, dan is het een ruit of een rechthoek.
e Een stomphoekige driehoek kan nooit een symmetrieas hebben.
f Een trapezium dat geen parallellogram is, heeft nooit een symmetrieas.
Vervolledig de figuur als je weet dat a een symmetrieas is.
a Hoeveel symmetrieassen heeft een regelmatige vijfhoek ?
b Hoeveel symmetrieassen heeft een regelmatige achthoek ?
c Hoeveel symmetrieassen heeft een regelmatige n -hoek ?
VALS
VALS
Hebben volgende figuren een symmetriemiddelpunt ?
a e i
b f j
Waar of vals ?
a Als een figuur een symmetriemiddelpunt heeft, dan heeft ze ook een eigendraaiing. WAAR VALS
b Als een figuur een eigendraaiing heeft, dan heeft ze ook een symmetriemiddelpunt. WAAR VALS
c Een regelmatige n -hoek heeft n – 1 eigendraaiingen.
WAAR VALS
Zin in een wel heel exotische bestemming ?
Vertrek aan het startpunt en volg op het spoor de juiste weg.
Als het figuurtje een symmetriemiddelpunt heeft, ga je rechtdoor.
Als de figuur geen symmetriemiddelpunt heeft, sla je rechts af.
Op die manier sprokkel je letters bij elkaar, die zelfs al in de juiste volgorde staan !
INKIJKEXEMPLAARDIEKEURE
De vakantiebestemming is :
1.6 Eigenschappen van transformaties
1 Transformaties van het vlak
In de vorige paragrafen heb je heel wat kunnen spiegelen, verschuiven, roteren en puntspiegelen. Voor elk punt had je precies één beeld.
Als je voor elk punt in het vlak precies één beeld vindt, dan spreken we over een transformatie van het vlak.
SPIEGELEN
A ligt niet op de as a.
Door A kun je maar één loodlijn tekenen op a .
Er is maar één punt A′ zodat a de middelloodlijn is van [ AA′].
Dus heeft A precies één beeld : A′ .
INKIJKEXEMPLAARDIEKEURE
a
B ligt op de spiegelas a.
Het beeld van B is B zelf en is dus enig.
Besluit :
Elk punt van het vlak heeft precies één beeld bij de spiegeling om a Een spiegeling is een transformatie van het vlak.
X heeft maar één beeld Y door de translatie volgens −→ AB
Door X kun je maar één evenwijdige tekenen aan AB en hierop ligt maar één punt Y zodat | AB | = | XY | en −→ AB dezelfde zin heeft als −→ XY .
A is niet het centrum van de rotatie.
Teken een cirkelboog met middelpunt O en straal | OA | Er bestaat steeds één punt A′ zodat AOA ′ = α en | OA′ | = | OA |.
Besluit :
Elk punt van het vlak heeft door de translatie over −→ AB precies één beeld. Een translatie is een transformatie van het vlak.
O is het centrum van de rotatie. Het beeld van O is O zelf en is dus enig.
Besluit :
Elk punt van het vlak heeft door de rotatie met centrum O en draaiingshoek a precies één beeld. Een rotatie is een transformatie van het vlak.
Merk op :
Een puntspiegeling is een speciale rotatie en dus ook een transformatie van het vlak.
eigenschap
Een spiegeling, translatie, rotatie en puntspiegeling zijn transformaties van een vlak.
Naast het spiegelen, verschuiven en roteren bestaan er nog andere transformaties van het vlak.
Voorbeelden : GLIJSPIEGELING
INKIJKEXEMPLAARDIEKEURE
Transformaties
Het woord ‘transformatie’ hebben we geleend van het Latijnse ‘transformatio’. Dat betekent gedaanteverwisseling.
De betekenis wordt beter geïllustreerd in de fysica (wetenschappen), waar bijvoorbeeld een transformator elektrische spanning omzet.
2 Op zoek naar eigenschappen
We gaan op zoek naar enkele eigenschappen van de geziene transformaties van het vlak.
a Voer deze onderzoeken uit in vier aparte bestanden
ONDERZOEK SPIEGELEN
ONDERZOEK VERSCHUIVEN
ONDERZOEK ROTEREN
ONDERZOEK PUNTSPIEGELEN
– Teken met ICT een parallellogram ABCD en een rechte a
– Teken een punt E dat collineair is met A en B.
– Spiegel het parallellogram ABCD en het punt E om a .
– Teken met ICT een parallellogram ABCD en een vector −→ GH.
– Teken een punt E dat collineair is met A en B.
– Teken het beeld van het parallellogram ABCD en het punt E over de vector −→ GH
– Teken met ICT een parallellogram ABCD en een punt O.
– Teken een punt E dat collineair is met A en B.
– Teken het beeld van het parallellogram ABCD en het punt E door de rotatie rond O over een hoek.
– Teken met ICT een parallellogram ABCD en een punt O.
– Teken een punt E dat collineair is met A en B.
– Spiegel het parallellogram ABCD en het punt E om O.
Voer nu op de gemaakte bestanden volgende opdrachten uit. Versleep dan een van de punten van de oorspronkelijk getekende figuur en ga na welke gegevens steeds aan elkaar gelijk zijn of welke eigenschappen steeds geldig blijven.
– I Meet de zijden van de gegeven figuur en de zijden van het beeld.
– II Controleer de evenwijdigheid van rechten bij de gegeven figuur en bij het beeld.
– III Meet de hoeken in beide figuren. Is de oriëntatie dezelfde gebleven?
– IV Ga na of het beeld van E collineair is met de beelden van A en B.
V Bereken de oppervlakte van beide figuren.
b Voer deze onderzoeken uit in één bestand
ONDERZOEK SPIEGELEN –
Teken met ICT een rechte a . Teken ook een spiegelas k – Spiegel de rechte a om k
ONDERZOEK VERSCHUIVEN – Teken ook een vector −→ GH
ONDERZOEK ROTEREN
INKIJKEXEMPLAARDIEKEURE
Verschuif de rechte a over de vector −→ GH.
Teken met ICT een punt O. – Teken het draaibeeld van de rechte a door de rotatie rond O over 60 °.
ONDERZOEK PUNTSPIEGELEN –
Teken het spiegelbeeld van de rechte a om O.
– VI Is het beeld van een rechte evenwijdig met de oorspronkelijke rechte ?
Ga dit na door in het algebravenster in te vullen : ZijnEvenwijdig ( …, …)
Je krijgt dan als antwoord true als de genoteerde rechten tussen haakjes evenwijdig zijn.
Je krijgt false als ze niet evenwijdig zijn.
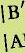
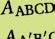
Vul op de fiches je bevindingen in voor een door jou gekozen situatie.
PUNTSPIEGELING
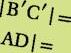
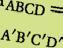
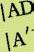
Bij een spiegeling, translatie, rotatie en puntspiegeling : – is de lengte van het oorspronkelijke lijnstuk gelijk aan de lengte van het beeld van dit lijnstuk ; – zullen evenwijdige rechten als beeld ook evenwijdige rechten opleveren ; – is de grootte van een hoek gelijk aan de grootte van het beeld van die hoek ; – blijft de oppervlakte van de oorspronkelijke figuur en het beeld dezelfde.
Bovendien zijn het schuifbeeld van een rechte en het spiegelbeeld om een punt van een rechte telkens rechten evenwijdig aan de oorspronkelijke rechte.
We vatten dit samen in deze eigenschappen :
eigenschappen
Elke spiegeling, translatie, rotatie en puntspiegeling behoudt : – de lengte van een lijnstuk (of de afstand) ; – de evenwijdigheid van rechten ; – de grootte van een hoek ; – de collineariteit ; – de oppervlakte van een figuur.
Het schuifbeeld van een rechte is een evenwijdige rechte. Het spiegelbeeld van een rechte om een punt is een evenwijdige rechte.
Gevolg: aangezien een spiegeling, translatie, rotatie en puntspiegeling de grootte van een hoek behouden, zullen ze ook de loodrechte stand behouden.
Merk op :
Translaties, rotaties en spiegelingen om een punt behouden de oriëntatie (of doorloopzin). Spiegelingen om een as behouden de oriëntatie (of doorloopzin) niet.
3 Samenvatting
INKIJKEXEMPLAARDIEKEURE
• Je kunt verklaren waarom een spiegeling, translatie, rotatie en puntspiegeling transformaties zijn van het vlak.
• Je kunt de eigenschappen van een spiegeling, translatie, puntspiegeling en rotatie verwoorden.
Elke spiegeling, translatie, rotatie en puntspiegeling behoudt : – de lengte van een lijnstuk (of de afstand) ; – de evenwijdigheid van rechten ; – de grootte van een hoek ; – de collineariteit ; – de oppervlakte van een figuur.
Het schuifbeeld van een rechte is een evenwijdige rechte. Het spiegelbeeld van een rechte om een punt is een evenwijdige rechte.
• Je kunt bovenstaande eigenschappen illustreren met ICT.
4 Oefeningen
Elke tekening illustreert een bepaalde eigenschap. Verwoord telkens de geïllustreerde eigenschap.
Transformaties van het vlak uitvoeren, steunend op eigenschappen.
a De twee rechten a en b staan loodrecht op elkaar. Verschuif de hele tekening over AB. Gebruik zo weinig mogelijk vectoren.
c A′ is het beeld van A onder een spiegeling om een punt O. Voer de volledige puntspiegeling uit zonder het punt O te plaatsen.
Noteer de eigenschap die je hebt toegepast.
Noteer de eigenschap die je hebt toegepast.
b Teken het schuifbeeld van het vierkant PQRS over de vector AB door zo weinig mogelijk vectoren te tekenen.
d [ A′D′] is het beeld van [ AD] onder een rotatie rond M over –90°. Voer de volledige rotatie uit zonder het punt O te plaatsen.
Noteer de eigenschap die je hebt toegepast.
Noteer de eigenschap die je hebt toegepast.
Bereken de oppervlakte van de gekleurde figuur als je weet dat | DC | = | AD |
Verklaar jouw werkwijze met behulp van de eigenschappen van transformaties.
cm
Verklaar waarom er geen spiegeling, translatie of rotatie bestaat zodat c ′ het beeld is van c
Geef drie verschillende translaties
t1, t2 en t3 zodat a ′ steeds het beeld is van a door die translatie.
Bepaal een translatie t zodat
t ( a ) = a ′
t ( b ) = b ′
Kan de ene vierhoek het beeld zijn van de andere vierhoek door een transformatie van het vlak ? Zo ja, geef enkele mogelijkheden. Geef telkens alle kenmerken van de transformatie.
Bepaal de translatie die de halfrechte [ AB afbeeldt op de halfrechte [ CD.
Kan A′B′C′D′ het beeld zijn van ABCD door een bepaalde translatie ? Verklaar.
a Hoeveel puntspiegelingen bestaan er die de rechte a afbeelden op de rechte a ′ ?
b Wat is er speciaal aan de ligging van de centra ?
JA NEEN JA NEEN
Verklaar waarom een spiegeling het midden van een lijnstuk bewaart.
Bereken de oppervlakte van D ABC als je weet dat sa ( D ABC) = D A′B′C′ Verklaar je werkwijze.
Teken met ICT een driehoek ABC en de zwaartelijn [ AM]. Kies een centrum O. Teken een schuifknop a die varieert van 0 ° tot 180 ° met een stapgrootte van 1°. Beschouw r = r ( O, a) .
a Zoek r ( D ABC).
b Zoek r ([ AM])
c Is [ A′M′] een zwaartelijn in D A′B′C′ ? Verklaar.
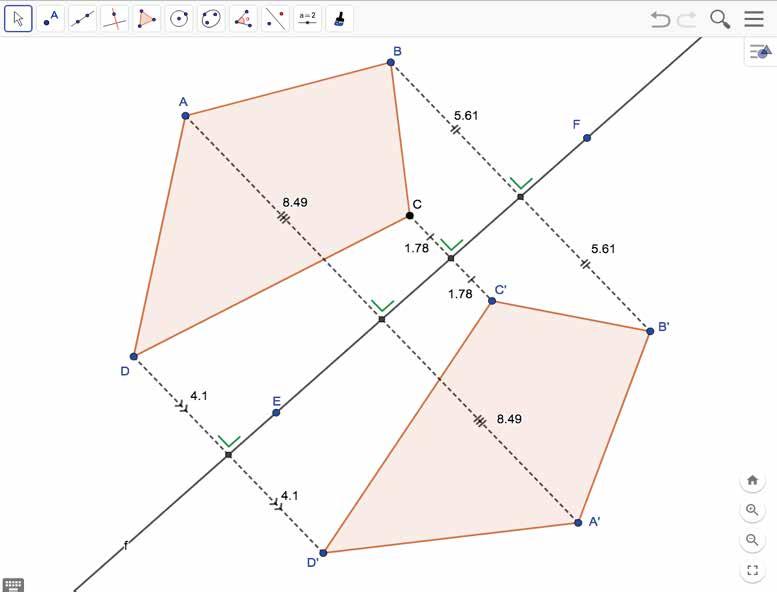
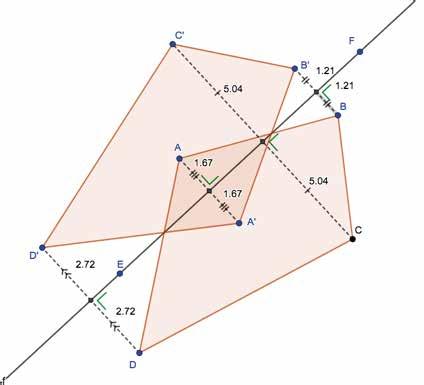
Spiegelen om een vierkant. Gegeven is een vierkant ABCD. Het punt O is het snijpunt van de diagonalen. Om het beeld te zoeken van een punt P verbind je O met P en neem je het ‘kortstbijzijnde’ snijpunt S met het vierkant ABCD. Pas de afstand | PS | af langs de andere kant van S. Zo krijg je P′. Spiegel als het ware P om het vierkant ABCD. Zoek nu het beeld van een rechte door zo’n spiegeling.
1.7
Verband tussen coördinaten in een assenstelsel en transformaties
INKIJKEXEMPLAARDIEKEURE
We bestuderen de verbanden die er zijn tussen coördinaten in een assenstelsel en de reeds gekende transformaties. We werken steeds in een orthonormaal assenstelsel (ook cartesiaans assenstelsel genoemd). De assen staan dan loodrecht op elkaar en de eenheden op beide assen zijn gelijk.
1 Samenhang tussen spiegelingen en coördinaten van punten
spiegeling om de x -as
D(2, 3)
A(–4, 2)
A′(–4, –2)
B(0, 0)
B′ y x 01 1
C(5, 0) = C′
COÖRDINAAT VAN HET PUNT
D′(2, –3)
spiegeling om de y -as
C′ (–2, 5 ) A′ (–6, –3 ) A (6, –3) C (2, 5) x y B (0, 1 ) = B′
COÖRDINAAT VAN HET
SPIEGELBEELD
( –4, 2) ( –4, –2) ( 0, 0) ( 0, 0) ( 5, 0) ( 5, 0) ( 2, 3) ( 2, –3)
Besluit : co( A) = ( x , y ) ⟹ co( sx ( A)) = ( x , –y )
Bij een spiegeling om de x -as verandert het tweede coördinaatgetal van toestandsteken.
COÖRDINAAT VAN HET PUNT
COÖRDINAAT VAN HET
SPIEGELBEELD ( 6, –3) ( –6, –3) ( 0, 0) ( 0, 0) ( 0, 1) ( 0, 1) ( 2, 5) ( –2, 5)
Besluit : co( A) = ( x , y ) ⟹ co( sy ( A)) = ( –x , y )
Bij een spiegeling om de y -as verandert het eerste coördinaatgetal van toestandsteken.
spiegeling om de eerste en de tweede bissectrice
De eerste bissectrice is de bissectrice van de hoek die bepaald wordt door de positieve delen van de x -as en y -as. Als je in de oorsprong op de eerste bissectrice de loodlijn tekent, dan bekom je de tweede bissectrice We spiegelen eerst om de eerste bissectrice.
COÖRDINAAT VAN HET PUNT
COÖRDINAAT VAN HET SPIEGELBEELD
INKIJKEXEMPLAARDIEKEURE
(–5, 2)
′(–5, –3)
(–3,–5)
′(1, 3)
(0, 2)
′(2, 0)
(3, 1)
( 3, 1) ( 1, 3)
( 0, 2) ( 2, 0)
( –5, 2) ( 2, –5)
( –3, –5) ( –5, –3)
Besluit : co( A) = ( x , y ) ⟹ co( sa ( A)) = ( y , x )
′(2,–5)
Wat gebeurt er na een spiegeling om de tweede bissectrice ?
Bij een spiegeling om de eerste bissectrice wisselen de coördinaatgetallen van plaats.
COÖRDINAAT VAN HET PUNT
(0, 3)
(3, 2)
′(–3, 0)
5 –4 –3 –2 –
′(3, –1)
′(5, –1) B′(–2, –3)
(1, –3)
(1, –5)
COÖRDINAAT VAN HET
( 0, 3) ( –3, 0) ( 3, 2) ( –2, –3) ( 1, –3) ( 3, –1) ( 1, –5) ( 5, –1)
Besluit : co( A) = ( x , y ) ⟹ co( sb ( A)) = ( –y , –x )
Bij een spiegeling om de tweede bissectrice wisselen de coördinaatgetallen van plaats en veranderen beide coördinaatgetallen van toestandsteken.
2 Samenhang tussen translaties en coördinaten van punten
translatie over een vector evenwijdig met de x -as
P(–2, 4)
A(–4, 2)
C(–3, –3)
A′(1, 2)
Q(3, 4)
10 1 y x B′(7, 0)
B(2, 0)
C′(2, –3)
translatie over een vector evenwijdig met de y -as
D(0, 5)
A(–4, 2)
P(–1, 2)
D′(0, 2)
10 1 y x
B(2, 0)
A′(–4, –1)
Q(–1, –1)
C(5, 3)
C′(5, 0)
B′(2, –3)
translatie over een vector niet evenwijdig met de x -as of de y -as
COÖRDINAAT VAN HET PUNT
COÖRDINAAT VAN HET
SCHUIFBEELD
( –2, 4) ( 3, 4)
( –4, 2) ( 1, 2)
( 2, 0) ( 7, 0)
( –3, –3) ( 2, –3)
INKIJKEXEMPLAARDIEKEURE
P(–2, 3)
A′(–1, 2)
A(–4, 1)
Q(1, 4)
X(1, 3)
10 1 y x C(2, 0)
B′(0, –1)
B(–3, –2)
C′(5, 1)
Besluit :
PQisnaarrechtsgeoriënteerd:
co(A )=( x + | PQ |, y )
PQisnaarlinksgeoriënteerd:
co(A )=( x −| PQ |, y )
COÖRDINAAT VAN HET PUNT COÖRDINAAT VAN HET
Besluit :
SCHUIFBEELD
( –4, 2) ( –4, –1) ( 2, 0) ( 2, –3) ( 5, 3) ( 5, 0) ( 0, 5) ( 0, 2)
PQisnaarondergeoriënteerd:
co(A )=( x , y −| PQ |)
PQisnaarbovengeoriënteerd:
co(A )=( x , y + | PQ |)
COÖRDINAAT
( –2, 3) ( 1, 4)
( –4, 1) ( –1, 2) ( –3, –2) ( 0, –1) ( 2, 0) ( 5, 1)
Besluit : eerste coördinaatgetal : +3 tweede coördinaatgetal : +1
Merk op : Eentranslatieovereenvectornietevenwijdigmetde x -asofde y -asiseensamenstellingvaneentranslatie
−→ PXovereenvectorevenwijdigmetde x -aseneentranslatie −→ XQovereenvectorevenwijdigmetde y -as(of omgekeerd).
3 Samenhang tussen puntspiegeling en coördinaten van punten
puntspiegeling om de oorsprong
C′(0, –3) A′(–6, 3) D′(–2, –5) y x 10
D(2, 5)
C(0, 3)
B(0, 0) = B′
A(6, –3)
COÖRDINAAT VAN HET PUNT
COÖRDINAAT VAN HET
SPIEGELBEELD
( 6, –3) ( –6, 3) ( 0, 0) ( 0, 0) ( 0, 3) ( 0, –3) ( 2, 5) ( –2, –5)
Besluit :
co (A)=( x , y )=⇒ co sO (A) =( x , y )
INKIJKEXEMPLAARDIEKEURE
Merk op :
Een puntspiegeling om de oorsprong is een samenstelling van een spiegeling om de x -as en een spiegeling om de y -as (of omgekeerd).
4 Samenvatting
• Je kunt de samenhang illustreren en bespreken tussen transformaties en de coördinaten van een punt en zijn beeld.
SPIEGELING om de x -as
SPIEGELING om de y -as
SPIEGELING om de eerste bissectrice a
SPIEGELING om de tweede bissectrice b
SPIEGELING om de oorsprong
co (A)=( x , y )=⇒ co s x (A) =( x , y )
co (A)=( x , y )=⇒ co s y (A) =( x , y )
co (A)=( x , y )=⇒ co sa (A) =( y , x )
co (A)=( x , y )=⇒ co s b (A) =( y , x )
co (A)=( x , y )=⇒ co sO (A) =( x , y )
• Je kunt de coördinaat van het beeld van een punt bepalen als een translatie over de x -as of de y -as gegeven is.
• Je kunt de coördinaat van het beeld van een punt bepalen als een willekeurige translatie gegeven is.
5 Oefeningen
In een orthonormaal assenstelsel zijn deze punten gegeven : A( –3, 2) , B( 5, 0) , C( 3, 3) en D( 2, –1)
Gevraagd : spiegel die punten om de x -as, de y -as en de oorsprong O van het assenstelsel en bepaal telkens de coördinaten van de beeldpunten
–3, 2)
5, 0)
3, 3)
2, –1)
coördinaat na spiegeling om de x -as
coördinaat na spiegeling om de y -as
coördinaat na spiegeling om O
In een orthonormaal assenstelsel zijn deze punten gegeven : A( –3, 2) , B( 5, 0) , C( 3, 3) en D( 2, –1)
Gevraagd : spiegel de punten A, B, C en D om de eerste en de tweede bissectrice van het assenkruis en bepaal telkens de coördinaten van de beeldpunten
A( –3, 2)
B( 5, 0)
C( 3, 3)
D( 2, –1)
coördinaat na spiegeling om de eerste bissectrice coördinaat na spiegeling om de tweede bissectrice
In een orthonormaal assenstelsel zijn deze punten gegeven : A( –3, 2) , B( 5, 0) , C( 3, 3) en D( 2, –1) P( 2, 4) en Q( –4, 4)
Gevraagd : zoek de beeldpunten van A, B, C en D door de translatie over de vector −→ PQ
A( –3, 2)
B( 5, 0)
C( 3, 3)
D( 2, –1)
coördinaat na translatie over −→ PQ
In een orthonormaal assenstelsel zijn deze punten gegeven : A( –3, 2) , B( 5, 0) , C( 3, 3) en D( 2, –1) M( 1, –1) en N( 1, 2)
Gevraagd : zoek de beeldpunten van A, B, C en D door de translatie bepaald door de vector −−→ MN
A( –3, 2)
B( 5, 0) C( 3, 3) D( 2, –1)
coördinaat na translatie over −→ MN
In een orthonormaal assenstelsel zijn deze punten gegeven : A( –3, 6) , B( 4, 1) en C( –5, –4)
Gevraagd : bepaal de coördinaten van de draaibeelden van A, B en C na rotatie rond de oorsprong O over 90 ° en over –90 °
A( –3, 6)
coördinaat na rotatie rond O over 90 °
coördinaat na rotatie rond O over –90 °
B( 4, 1) C( –5, –4)
In een orthonormaal assenstelsel zijn deze punten gegeven : A( 4, 2), B( –2, 6) en C( –1, –3) a is de eerste bissectrice
Gevraagd : bepaal de coördinaat van de volgende punten
a sx ( A)
f r ( O, –90°)( B)
b sa ( A) g sO( B)
c r ( O, 90°)( B) h t −→ AB (C)
d t −→ CB (A) i sy ( B)
e sa ( C)
In een orthonormaal assenstelsel zijn deze punten gegeven : A( 4, 3), B ( –2, 4), C ( 3, –2) P( –1, 2), Q ( 1, –3)
D ABC
Gevraagd : bepaal de coördinaat van de hoekpunten van het beeld van D ABC
A′)
a t −→ PQ
b t −→ QP
c t −→ AB
d sO
e r ( O, 90°)
f r ( O, –90°)
B′)
C′)
In een orthonormaal assenstelsel zijn deze punten gegeven : P( –3, 0) , Q( –3, 4) en R( 1, 4)
D PQR
Gevraagd : bepaal het beeld A( 2, 2) van D PQR en bepaal de coördinaten van alle beeldpunten door volgende transformaties uit te voeren a t −→ OA b sx c sy d sO
P( –3, 0) Q( –3, 4) R( 1, 4)
coördinaat van het beeldpunt onder transformatie t −→ OA
coördinaat van het beeldpunt onder transformatie sx
coördinaat van het beeldpunt onder transformatie sy coördinaat van het beeldpunt onder transformatie s O
In een orthonormaal assenstelsel is ABCD een parallellogram gegeven met A( –10, 12) , B( 5, 7) en C( –2, –1)
Gevraagd :
a Bepaal co(D)
b Welke transformatie kun je gebruiken om die coördinaat te vinden ?
Kruis alle mogelijkheden aan en specificeer.
o Een spiegeling om een as
Indien ja, noteer hier de spiegelas :
o Een translatie
Indien ja, noteer hier een vector:
o Een rotatie
Indien ja, noteer hier het centrum en de draaiingshoek :
o Een spiegeling om een punt
Indien ja, noteer hier het centrum :
In een orthonormaal assenstelsel is het vierkant ABCD gegeven met A( 0, 4), B( 2, 4) en C( 2, 2)
Van een ander vierkant ken je van slechts twee hoekpunten de coördinaten: ( 6, 4) en ( 8, 4).
Noteer drie verschillende transformaties die ABCD afbeelden op het andere vierkant.
Vaardigheden | Een transformatie is niet altijd een isometrie
Een transformatie waarbij de afmetingen en vorm bewaard worden, noemen we een isometrie
Op blz. 53 maakte je al kennis met andere dan de bestudeerde transformaties. We bekijken opnieuw de homothetie en de evenwijdige projectie. Dit zijn transformaties maar geen isometrieën. Bestudeer elk van deze transformaties. Je herkent de eerder bestudeerde eigenschappen. Kruis telkens aan als de eigenschap geldt.
HOMOTHETIE
Je ziet hier een homothetie met centrum O en schaalfactor 2.
Deze transformatie beeldt een vlakke figuur af op een gelijkvormige figuur (schaalmodel).
- Bij een schaalfator tussen 0 en 1 is het beeld een verkleinde figuur.
- Bij een schaalfactor groter dan 1 is het beeld een vergrote figuur.
- Is de schaalfactor 1 dan is het beeld een exacte kopie, het heeft dezelfde vorm en grootte : een congruente figuur. Je bestudeert homothetieën in het derde jaar.
EVENWIJDIGE PROJECTIE
deze transformatie behoudt de ...
Alle punten van de figuur worden geprojecteerd op een rechte volgens een bepaalde richting. De projectielijnen zijn evenwijdig. Evenwijdige projectie is een transformatie die je kan gebruiken om schaduwen te tekenen. Maar dit wordt ook gebruikt in technologie, fotografie, kaarten, …
Ook deze transformatie bestudeer je in het derde jaar.
... lengte
... evenwijdigheid
... grootte van een hoek
... collineariteit
... oppervlakte
... oriëntatie
deze transformatie behoudt de ...
... lengte
... evenwijdigheid
... grootte van een hoek
... collineariteit
... oppervlakte
... oriëntatie
dit moet ik leren pagina ik ken het ! oké voor examen
❒ Ik kan een figuur spiegelen om een as. 11 J J
❒ Ik weet wat een vector is. 19 J J
❒ Ik weet wat gelijke vectoren zijn. 20 J J
❒ Ik kan een figuur verschuiven over een vector. 22 J J
❒ Ik weet wat een georiënteerde hoek is. 29 J J
❒ Ik kan een figuur roteren om een punt over een gegeven hoek. 31 J J
❒ Ik kan een figuur spiegelen om een punt. 34 J J
❒ Ik weet wanneer een figuur spiegelsymmetrisch om een as is.
❒ Ik kan in een figuur de symmetrieassen bepalen.
❒ Ik weet wanneer een figuur spiegelsymmetrisch om een punt is.
❒ Ik kan in een figuur het symmetriemiddelpunt bepalen.
❒ Ik weet wanneer een figuur draaisymmetrisch is.
❒ Ik kan in een figuur de eigendraaiingen bepalen.
❒ Ik ken de eigenschappen van een spiegeling, translatie, rotatie en puntspiegeling, en kan ze herkennen en toepassen.
❒ Ik kan de samenhang illustreren tussen transformaties en de coördinaten van een punt en zijn beeld.
Transformaties 1 INKIJKEXEMPLAARDIEKEURE
43 J J
43 J J
44 J J
44 J J
44 J J
44 J J
56 J J
63 J J
❒ Ik weet dat er andere transformaties zijn waarbij niet alle bestudeerde eigenschappen gelden. 70 J J
a Teken D ABC met co( A) = ( 1, 2) , co( B) = ( 7, 6) en co( C) = ( 3, –1)
b Spiegel die driehoek om de y -as.
c Noteer de coördinaten van A′, B′ en C′ .
Transformaties 1 INKIJKEXEMPLAARDIEKEURE
d Wat kun je besluiten i.v.m. de coördinaten na een spiegeling om de y -as ?
a Teken een parallellogram EFGH waarvan E( –4, 2) , F( 1, 2) en G( 4, –4) drie hoekpunten zijn.
b Wat is de coördinaat van het vierde hoekpunt H ?
c Verschuif het parallellogram over −→ EG .
3 /
a Teken een rechthoek PQRS met co( P) = ( 2, –5) , co( Q) = ( –2, –4) , co( R) = ( 0, 4) en co( S) = ( 4, 3)
b Roteer de rechthoek rond R over een hoek van 180 °.
c Welke figuur is S′Q′SQ ?
d Wat is er bijzonder aan de diagonalen van vierhoek S′Q′SQ ?
Vul het passende antwoord in.
4 / 10
a s BE( C) =
b t −→ GE ( D) =
c s B( C) =
d r ( D,–60°)( B) =
e s ( H) = B
f s DE( ) = F
g t −→ AD ( ) = E
h r ( D,120°)( ) = E
i t −→ EH( DABD) =
j t −→ DD( G) =
INKIJKEXEMPLAARDIEKEURE
Welke drie eigenschappen herken je ?
5 / 3
Symmetrie in logo’s van automerken.
/ 3
INKIJKEXEMPLAARDIEKEURE
a Teken indien mogelijk de symmetrieassen van elk logo.
b Welke van bovenstaande logo’s zijn spiegelsymmetrisch om een punt ?
c Welke van bovenstaande logo’s zijn draaisymmetrisch om een punt ?
7 / 2
Waar of vals ?
a Elke translatie bewaart de oppervlakte van een figuur.
b Het draaibeeld van een rechte is een evenwijdige rechte.
c Er bestaan transformaties van het vlak die een cirkel niet afbeelden op een cirkel.
d Een regelmatige n -hoek heeft ( n – 1) eigendraaiingen.
e Een gelijkbenig trapezium heeft een symmetriemiddelpunt.